最长回文子串
给定一个字符串 s，找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000
示例 1：
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
暴力超时版
const longestPalindrome_overtime = (str = '') => {
const judgePalindrome = (str) => {
const mid = ~~(str.length/2), l = str.length - 1
let i = 0
while (i <= mid) {
const s = str[i], e = str[l - i]
if(s !== e) return false
i++
}
return true
}
let max = str[0] || ''
for(let i=0; i< str.length - 1; i++) {
let s = str[i]
let e = ''
for(let j = i + 1; j< str.length; j++) {
e += str[j]
const ss = s + e
if(judgePalindrome(ss) && ss.length >= max.length) max = ss
}
}
return max
}
动态规划版
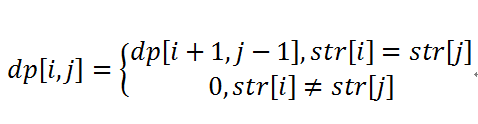上面的状态转移方程表示，当str[i]=str[j]时，如果str[i+1...j-1]是回文串，则str[i...j]也是回文串；如果str[i+1...j-1]不是回文串，则str[i...j]不是回文串。单个字符，两个相同字符都是回文串。
核心在于 dp[i][j] == dp[i+1][j-1] && s[i] === s[j]
动态规划 DP版
export const longestPalindrome_DP = (str = '') => {
const len = str.length
const dp = []
let max = -1, maxStr = ''
for(let i = 0; i < len; i++) {
dp[i] = []
}
for(let k = 0; k < len; k++){
// k为所遍历的子串长度 - 1，即左下标到右下标的距离
for(let i = 0; i + k < len; i++){
let j = i + k;
// i为子串开始的左下标，j为子串开始的右下标
if(k == 0){
dp[i][j] = true; // 当子串长度为1时，必定是回文
} else if(k <= 2){
// 当子串长度为2时，两字符相同则符合回文，长度为3，首位字符相同则符合回文
if(str[i] == str[j]){
dp[i][j] = true;
}else{
dp[i][j] = false;
}
} else {
// 当子串长度超过3，取决于去掉头尾之后的子串是否回文并且首位字符是否相同
if(dp[i+1][j-1] && (str[i] == str[j])) {
dp[i][j] = true;
} else {
dp[i][j] = false;
}
}
if(dp[i][j] && k > max){
max = k;
maxStr = str.substring(i, j + 1)
}
}
}
return maxStr
}
中心扩展算法
export const longestPalindrome_ep = (str = '') => {
const expandArroundCenter = (str ='', l, r) => {
while (l >= 0, r < str.length && str[l] === str[r]) {
l--
r++
}
return r - l - 1
}
let maxStr = str[0] || ''
let start = 0, end = 0
for(let i = 0; i < str.length; i++) {
const len1 = expandArroundCenter(str, i, i)
const len2 = expandArroundCenter(str, i, i + 1)
const len = Math.max(len1, len2)
if(len >= end - start) {
start = i - (len - 1) / 2
end = i + len / 2
}
}
return str.substring(start, end + 1)
}
Manacher算法
Manacher算法，是一种线性时间的方法。引入一个技巧，可以使得奇数和偶数的情况统一处理
具体做法如下：abba转换为#a#b#b#a#
S | # | a | # | b | # | b | # | a | # |
|---|---|---|---|---|---|---|---|---|---|
| P | 1 | 2 | 1 | 2 | 5 | 2 | 1 | 2 | 1 |
S |
|---|
| P |
数组 P[i] 来记录以字符S[i]为中心的最长回文子串向左/右扩张的长度.
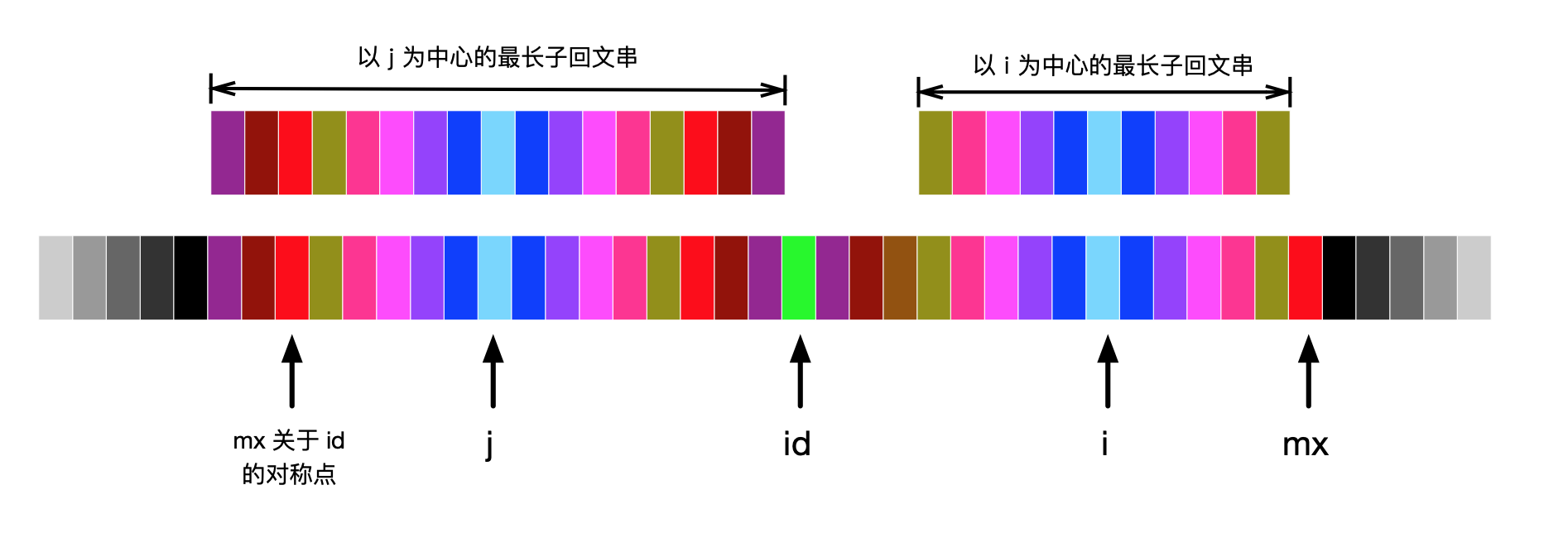
- id ：从开始到现在使用“中心扩散法”能得到的“最长回文子串”的中心的位置；
- mx：从开始到现在使用“中心扩散法”能得到的“最长回文子串”能延伸到的最右端的位置。容易知道 mx = id + p[id]。
export const longestPalindrome = (str) =>{
let maxlength = 1, maxStr = str[0] || ''
const P = []
// 1、id ：从开始到现在使用“中心扩散法”能得到的“最长回文子串”的中心的位置；
// 2、mx：从开始到现在使用“中心扩散法”能得到的“最长回文子串”能延伸到的最右端的位置。容易知道 mx = id + p[id]。
let id = 0, mx = 0
// 改造字符串
const nStr = Array.from(str).reduce((result, item) => {
result += `${item}#`
return result
}, '#')
// 初始化 P
for(let i = 0; i < nStr.length; i++)
P[i] = 0
for(let i = 0; i< nStr.length; i++) {
P[i] = i < mx ? Math.min(P[2 * id - i], mx - i) : 1
while (i - P[i] >= 0 && i + P[i] < nStr.length && nStr[i - P[i]] === nStr[i + P[i]]) P[i]++
if(i + P[i] > mx) {
mx = i + P[i]
id = i
}
if(P[i] - 1 >= maxlength) {
maxlength = P[i] - 1
maxStr = nStr.substring(i - P[i] + 1, i + P[i])
}
}
return maxStr.replace(/#/g, "")
}
console结果可能不准确，按F12打开控制台查看