寻找两个有序数组的中位数
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
示例
nums1 = [1, 3] nums2 = [2] 则中位数是 2.0
暴力法
// 合并数组,快速排序,奇偶差别,求求中位数
export const findMedianSortedArrays_overtime = (nums1 = [], nums2 = []) => {
const swap = (arr, i, j) => {
var temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
const insertSort = (arr = [], l = 1, r = arr.length - 1) => {
for (; l <= r; l++) {
let e = arr[l]
let j = l
for (; j > 0 && arr[j - 1] > e; j--) {
arr[j] = arr[j - 1]
}
arr[j] = e
}
return arr
}
const quickSort = (arr, l = 0, r = arr.length - 1) => {
if (r - l <= 10) {
return arr.sort((a, b) => a - b)
}
if (r - l > 10 && r - l <= 30) {
return insertSort(arr, l, r)
}
let randomIndex = Math.ceil(Math.random() * (r - l) + l)
swap(arr, l, randomIndex)
let v = arr[l],
lt = l, //arr[l+1,...lt]
gt = r + 1, // arr[gt,...r]
i = l + 1 // arr[lt+1,...i]
while (i < gt) {
if (arr[i] < v) {
swap(arr, i, ++lt)
i++
} else if (arr[i] > v) {
swap(arr, i, --gt)
} else {
i++
}
}
swap(arr, l, lt)
quickSort(arr, l, lt - 1)
quickSort(arr, gt, r)
return arr
}
const arr = quickSort([...nums1, ...nums2])
const m = ~~(arr.length / 2)
if (arr.length % 2 === 0) {
return (arr[m] + arr[m - 1]) / 2
} else {
return arr[m]
}
}
- 时间复杂度:数组sort,插入排序,快排 -> 最差O(n^2),平均 -> nlogn
- 空间复杂度:开辟了一个数组,保存合并后的两个数组 O(m+n)O(m+n)
- 不满足题目要求
寻K法
在两个有序数组中寻找合并排序后第K个元素,省去先排序再找,二分大法思想,每个数组中寻k/2

- 寻7除2求整,上下寻3

- 舍小留大,减3为4,二分重寻
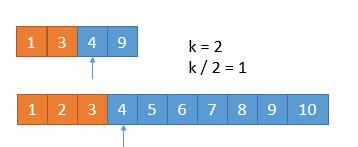
- 除2得2,5大3小,去上留下,减二二分为一。相等任意取一
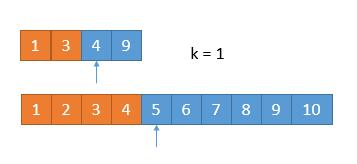
- 为1不分,取较小者

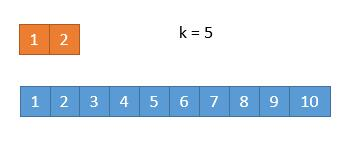
- k值二分大于其中一个数组的长度
1. 改变K值,根据对应情况移动数组起始点,再重新比较 2. K值与数组下标对应关系
3. 二分后新K值+起始坐标大于短数组的情况
4. 数组不是真的变短了,是比较时的起始坐标改动
5. 不同情况下K值减少的多少,什么情况该移动哪个数组起始下标,移动多少?
export const findMedianSortedArrays_merge = (nums1, nums2) => {
const getKth = (arr1, start1, end1, arr2, start2, end2, k) => {
const len1 = end1 - start1 + 1,
len2 = end2 - start2 + 1
if(len1 > len2) return getKth(arr2, start2, end2, arr1, start1, end1, k)
if(len1 === 0) return arr2[start2 + k - 1]
if(k === 1) return Math.min(arr1[start1], arr2[start2])
const mid = ~~(k/2), i = mid - 1, j = len1 - 1
if(start1 + mid > end1) {
if(arr1[end1] <= arr2[start2 + j]) {
start1 = end1 + 1
} else {
start2 += len1
}
k -= len1
return getKth(arr1, start1, end1, arr2, start2, end2, k)
}
if(arr1[start1 + i] > arr2[start2 + i]) start2 += mid
else start1 += mid
k -= mid
return getKth(arr1, start1, end1, arr2, start2, end2, k)
}
const n = nums1.length, m = nums2.length
const left = ~~((n + m + 1)/2),
right = ~~((n + m + 2)/2)
// 将奇偶情况合并,如果是奇数,会求两次同样的k
const l = getKth(nums1, 0, n -1, nums2, 0, m - 1, left)
const r = getKth(nums1, 0, n -1, nums2, 0, m - 1, right)
return (l + r) /2
}
时间复杂度:每进行一次循环,减少 k/2 个元素,所以时间复杂度是 O(log(k),而 k = (m+n)/2,所以最终的复杂也就是 O(log(m+n))
空间复杂度: O(1)
数学统计法
中位数是什么?即将一串数或者集合分成左右两个相等的部分
Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Arr1 | 1 | 1 | 2 | ||||||||
| Arr2 | 5 | 7 | 7 | 8 | 9 | 12 | |||||
| Arr1+Arr2 | 1 | 1 | 2 | 5 | 7 | 7 | 8 | 9 | 12 |
Index |
|---|
| Arr1 |
| Arr2 |
| Arr1+Arr2 |
肉眼观察:
- Arr1 + Arr2两个数组的中位数为 7
好像找不出什么规律?
肉眼再观察:
Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Arr1 | 1 | 3 | 4 | 5 | 7 | ||||||
| Arr2 | 2 | 3 | 3 | 4 | 7 | 12 | |||||
| Arr1+Arr2 | 1 | 2 | 3 | 3 | 3 | 4 | 4 | 5 | 7 | 7 | 12 |
Index |
|---|
| Arr1 |
| Arr2 |
| Arr1+Arr2 |
Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| Arr1 | 2 | 5 | 13 | 14 | ||||||
| Arr2 | 1 | 2 | 4 | 8 | 9 | 10 | ||||
| Arr1+Arr2 | 1 | 2 | 2 | 4 | 5 | 8 | 9 | 10 | 13 | 14 |
Index |
|---|
| Arr1 |
| Arr2 |
| Arr1+Arr2 |
也就是说我们将两个数组切成两段

m = arr1.length
n = arr2.length
切到某个i,j的时候,中位数在arr1[i],arr1[i+1],arr2[j],arr2[j+1]中的时候,i的左边和j的左边合成arr1+arr2的左半部分,i的右边和j的右边合成arr1+arr2的右半部分
当m+n为偶数的时候:
i + j = m - i + n - j, 也就是 j = (m + n) / 2 - i
中位数为 = (max(arr1[i-1],arr2[j-1]) + min(arr1[i], arr2)) /2
当m+n为奇数的时候: 左半部分的长度比右半部分大1
i+j = m - i + n - j + 1, j = (m + n + 1) / 2 - i
中位数为 = max(arr1[i -1], arr2[j - 1])
j合并为, j = ~~((m + n + 1) / 2) - i 为了保证 max ( arr1 [ i - 1 ] , arr2 [ j - 1 ])) <= min ( arr1 [ i ] , arr2 [ j ]))
当arr2[j-1] > arr1[i], i < m
当arr1[i-1] > arr2[j], i > 0
当i=0或者j=0, 当j=0,最大值就是arr1[i -1],当i=O,最大是就是arr2[j-1]
当i=m或者j=n,当i=m,最小值就是arr2[j],当j=n,最小值就是arr1[i]
初始化 i 为中间的值,然后减半找中间的,减半找中间的,减半找中间的直到答案。
初始i = ~~((0 + m + 1) / 2)
export const findMedianSortedArrays = (nums1, nums2) => {
const m = nums1.length, n = nums2.length
if(m > n) return findMedianSortedArrays(nums2, nums1)
let iMin = 0, iMax = m
while(iMin <= iMax) {
// 为了保证当m+n为奇数的时候: 左半部分的长度比右半部分大1
// iMin增大或,iMax减小。i , ~~(2iMax + 1) /2 ~ iMax || ~~((2iMin + 1)/2) ~ iMin
let i = ~~((iMin + iMax + 1) / 2), j = ~~((m + n + 1) / 2) - i
if(i < iMax && nums2[j -1] > nums1[i]) {
iMin = i + 1
} else if(i > iMin && nums1[i -1] > nums2[j]) {
iMax = i - 1
}else { // 达到要求, 边界单独考虑
let maxLeft, minRight
if(i === 0) maxLeft = nums2[j - 1]
else if(j === 0) maxLeft = nums1[i - 1]
else maxLeft = Math.max(nums1[i - 1], nums2[j - 1])
if(i === m) minRight = nums2[j]
else if(j === n) minRight = nums1[i]
else minRight = Math.min(nums1[i], nums2[j])
let mid
if(!maxLeft && maxLeft !== 0) maxLeft = minRight
if(!minRight && minRight !== 0) minRight = maxLeft
if((m + n) % 2 === 0) mid = (maxLeft + minRight) / 2
else mid = Math.min(maxLeft, minRight)
return mid
}
}
}
console结果可能不准确,按F12打开控制台查看
← 不含连续1的非负整数 四键键盘 →