最长上升子序列

• 给定一个无序的整数数组，找到其中最长上升子序列的长度。

示例1

输入: [10,9,2,3,7,5,101,6]
输出: 4 
解释: 最长的上升子序列是 [2,3,7,101]，它的长度是 4。

• [10,9,2,3,7,5,101,6]的最长子序列是[2,3,7,101]
• [10,9,2,3,7,5,101,6,1]的最长子序列也是[2,3,7,101]
• 无序数组的最长上升子序列是以nums[i]结尾的最长递增子序列的长度

动态规划

• 定义: dp[i] 表示以 nums[i] 这个数结尾的最长递增子序列的长度。
• 对于数组[10,9,2,3,7,5,101,6]
  • dp[0] = 1
  • dp[1] = 1
  • dp[2] = 1
  • dp[3] = 2 = dp[2] + 1
  • dp[4] = 3 = dp[3] + 1
  • dp[5] = 3 = dp[3] + 1
  • dp[6] = 4 = dp[4] + 1
• dp[i]=max(dp[j])+1,其中0≤j

dp[0] = 1(base)
# 进行状态转移
for 状态1 in 状态1的所有取值：
    dp[i] = base
    for 状态2 in 状态2的所有取值：
        dp[i] = max(dp[i], dp[j] + 1)

export const lengthOfLIS = nums => {
  const len = nums.length
  if (!len) return 0
  const dp = new Array(len).fill(1)

  for (let i = 0; i < len; i++) {
    for (let j = 0; j < i; j++) {
      if (nums[j] < nums[i]) {
        dp[i] = Math.max(dp[i], dp[j] + 1)
      }
    }
  }

  return Math.max.apply(null, dp)
}

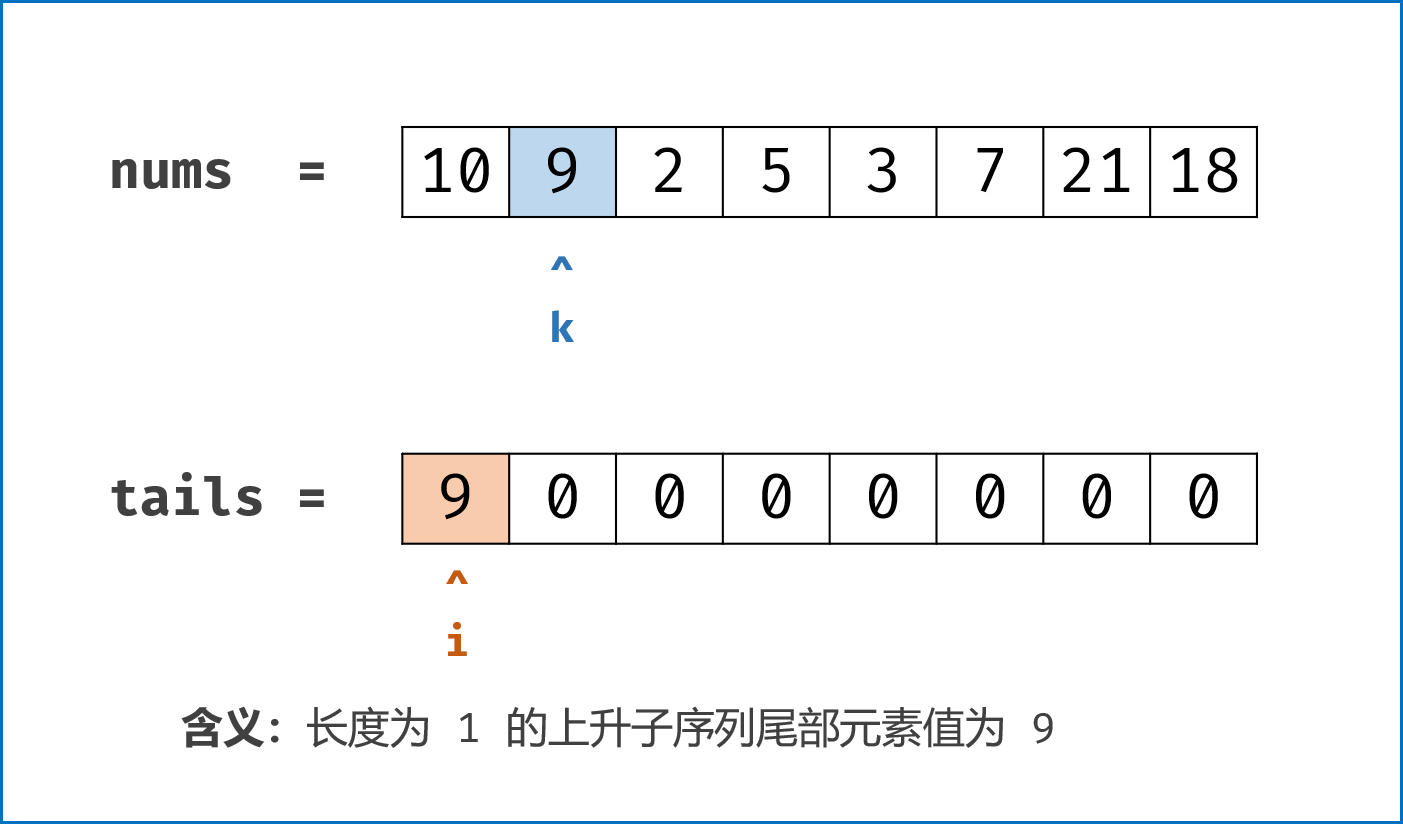
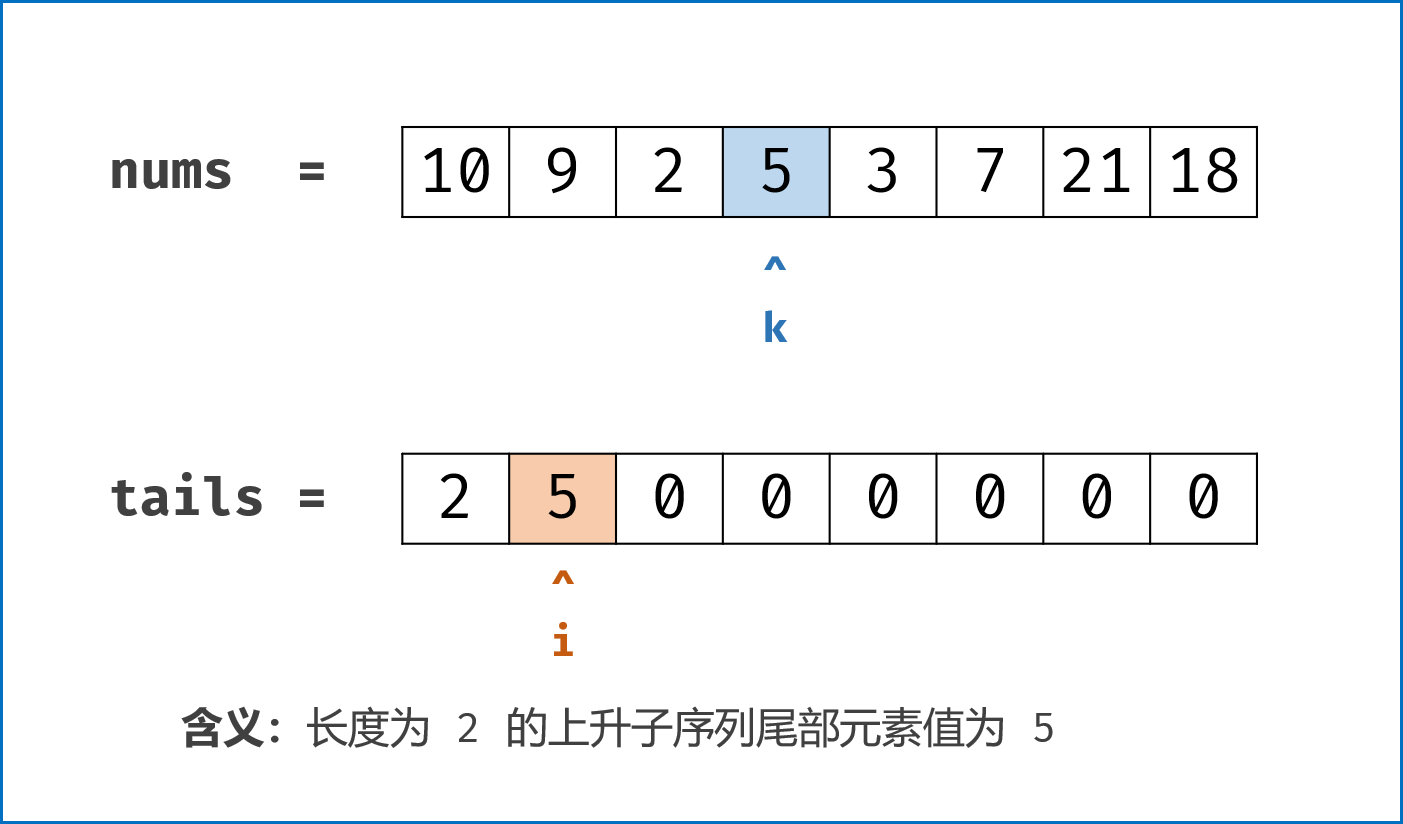
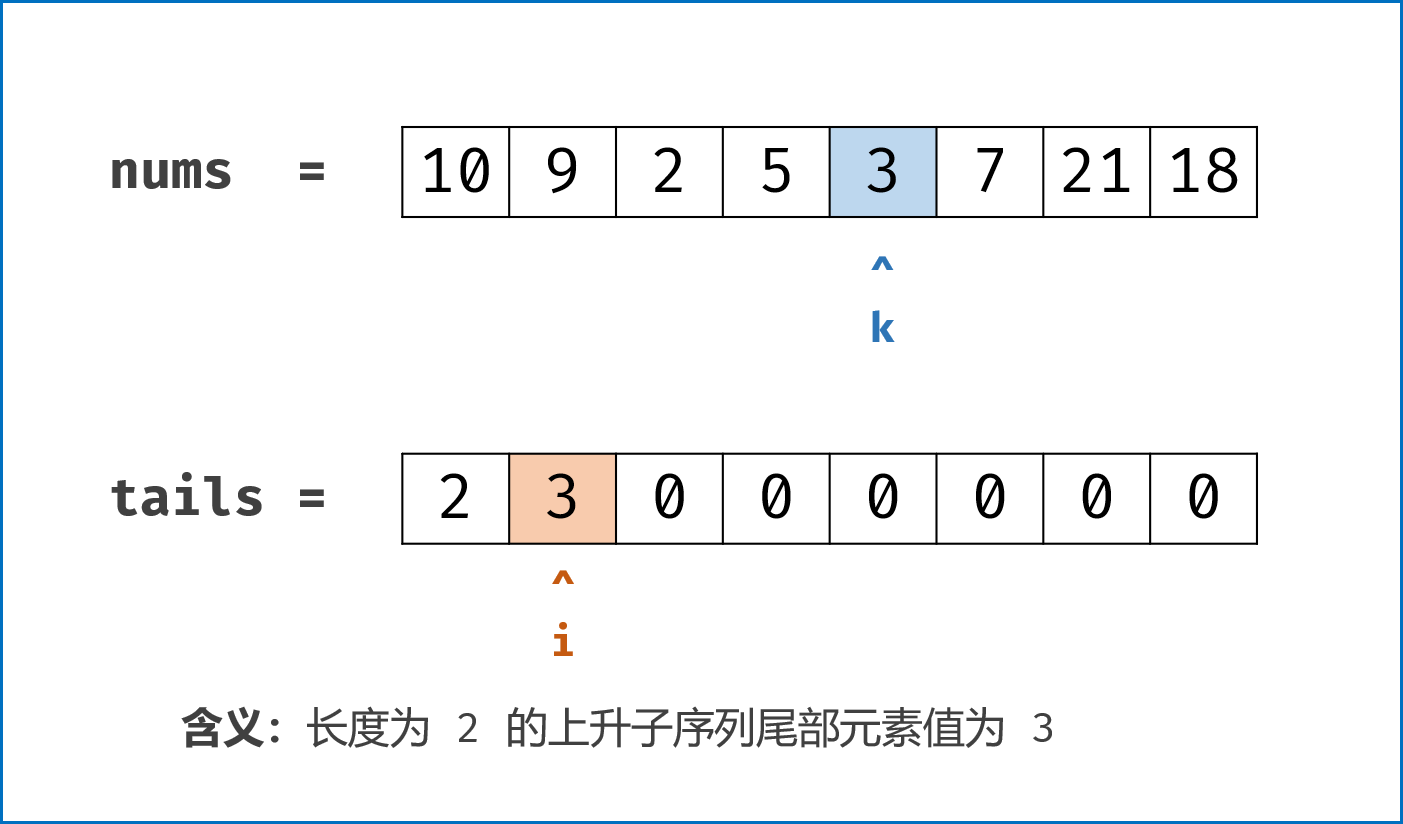
二分查找

• 维护一个最小上升dp

  • 遇到比dp末尾元素大的push
  • 否则，用它覆盖掉dp里比它大的元素中, 最小的那个。

• 纸牌的堆数就是最长递增子序列的长度

export const lengthOfLIS_binarySearch = nums => {
  const len = nums.length
  if (len <= 1) return len

  const dp = [nums[0]]
  let max = 1

  for (let i = 1; i < len; i++) {
    if (nums[i] > dp[max - 1]) {
      dp.push(nums[i])
      max++
    } else {
      let l = 0, r = max - 1
      let mid

      while (l < r) {
        mid = (l + r) >> 1
        if (dp[mid] < nums[i]) {
          l = mid + 1
        } else {
          r = mid
        }
      }

      dp[l] = nums[i]
    }
  }

  return max
}

console结果可能不准确，按F12打开控制台查看