大顶堆实现

堆的定义

• 堆是一颗完全二叉树
• 堆中某个节点的值总是不大于或不小于其孩子节点的值；
• 堆中每个节点的子树都是堆。

最大堆结构图示

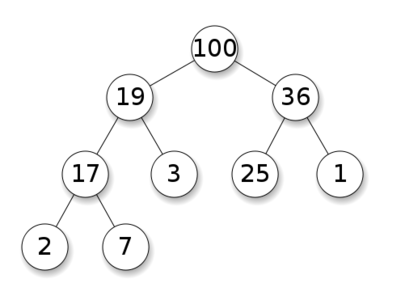
堆的操作与实现

export class MaxHeap {
  constructor(data = []) {
    Array.isArray(data) && (this.data = data)
    if (typeof data === 'number') {
      this.data = new Array(data)
    }
    this.count = 0
    this.init()
  }
  init() {
    this.buildMaxHeap(this.data)
  }
  swap(arr, m, n) {
    let temp = arr[m]
    arr[m] = arr[n]
    arr[n] = temp
  }
  buildMaxHeap(data = []) {
    for (let item of data) {
      if (!item && item !== 0) return
      this.insert(item)
    }
  }
  shiftUp(k) {
    // 如果一个节点比它的父节点大（最大堆）或者小（最小堆），那么需要将它同父节点交换位置。这样是这个节点在数组的位置上升
    while (k > 0 && this.data[~~(k / 2)] < this.data[k]) {
      this.swap(this.data, ~~(k / 2), k)
      k = ~~(k / 2)
    }
  }
  shiftDown(k) {
    // 如果一个节点比它的子节点小，那么需要将它向下移动
    while (k * 2 < this.count) {
      let j = k * 2
      if (j + 1 <= this.count && this.data[j + 1] > this.data[j]) j++
      if (this.data[k] >= this.data[j]) break
      this.swap(this.data, k, j)
      k = j
    }
  }
  insert(item) {
    // 在堆的尾部添加一个新的元素，然后使用 shiftUp 来修复对。
    if (this.count + 1 > this.data.length) throw Error('超过限制长度')
    this.data[this.count] = item
    this.shiftUp(this.count)
    this.count++
  }
  extractMax() {
    //取出最大数
    if (this.count === 0) return
    const ret = this.data[0]
    this.swap(this.data, 0, --this.count)
    this.data.splice(-1)
    this.shiftDown(0)
    return ret
  }
  sort() {
    const arr = [], reset = [...this.data]
    while (this.count !== 0) {
      const item = this.extractMax(),
        index = this.count
        arr[index] = item
    }
    this.count = reset.length
    this.data = reset
    return arr
  }
}

console结果可能不准确，按F12打开控制台查看